Quadratic map bifurcations
Qualitative change in iteration dynamics when parameter c is
changed is called bifurcation.
Tangent bifurcations
For c > 1/4 quadratic map iterations diverge to infinity.
At c = 1/4 the blue parabola touches the green diagonal and
attracting x1 and repelling x2
fixed points appear. This phenomenon is called the tangent bifurcation.
Drag the blue parabola by mouse.
To the left you see attracting period-3 orbit. In the center of the
right picture f o3(x) is similar to parabola therefore
the cycle is born in the tangent bifurcation at c = -1.75 and then
repeats all bifurcations of quadratic map.
Period doubling bifurcations
For c < -3/4 derivative in the left fixed point
f '(x•) = m < -1, i.e. the point becomes repelling.
In the vicinity of this fixed point after the first iteration perturbation
δx1 = mδx ~ -δx changes its sign but
after the second iteration
δx2 = m2δx ~ δx again.
Therefore an attracting period-2 orbit
xo → x1 → xo ...
appears. This phenomenon is called the period doubling bifurcation.
The second iteration of the map f o2(x)
(to the right above) has two attracting points (corresponding to
the stable cycle) and one unstable fixed point between them.
Note that near the center of the picture f o2(x) is
similar to parabola and under decreasing c will have period doubling
bifurcation again after which period-4 stable orbit appears and so on.
Unstable cycles never disappear more.
Bifurcation diagram for quadratic map
There is a good way to trace bifurcations of quadratic map on the (x, c)
plane by the bifurcation map (similar to the "logistic
bifurcation map"). Let us plot iterations fc: x1 = 0
→ x2 → x3 → ...→ xMaxIt
for all real c on the (x, c) plane. Colors (from blue to red)
show how often orbit visits the pixel (colors are changed under zooming).
Usually initial points are omitted but transient process shows how
fast iterations converge to an attractor.
You can watch iterations of fc(x) for corresponding
c values to the right.
Controls: Click mouse with Alt/Ctrl to zoom image.
Max number of iterations = 2000.
See coordinates of the image center and Δx,
Δc in the text field.
The vertical line goes through x = 0.
The top part of the picture begins with tangent bifurcation at c = 1/4.
For c > 1/4 points go away to infinity.
For -3/4 < c < 1/4 there is single attracting fixed point.
Filaments broadening show how the critical orbit points are attracted to
the fixed point. For c = 0 the fixed point coincides with the critical
one (the blue vertical line) and becomes superstable.
At c ~ -3/4 we see a branching point due to period doubling
bifurcation. After that the fixed point loses its stability and attracting
period-2 cycle appears. At c = -1 the cycle goes through the critical
point and becomes superstable and so on. Cascade of period doubling
bifurcations ends at c = -1.401155. Further you see region of chaotic
dynamics. It ends by crisis at c = -2. For c < -2 there
is an invariant Cantor set of unstable orbits with zero measure and
iterations of the critical point diverge.
In the chaotic band there are white narrow holes of windows of periodic
dynamics. The biggest one corresponds to period-3 window.
There are 3 junction regions in it and under iterations critical orbit
jumps sequentially between these regions.
The bifurcation map patterns
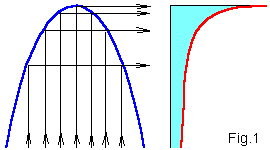 Fig.1 shows that caustics in distribution of points of chaotic orbits are
generated by an extremum of a map. Therefore singularities (painted in the
red) on the bifurcation diagram appear at images of the critical point
fc on(0).
Let us denote gn(c) = fcon(0), then
Fig.1 shows that caustics in distribution of points of chaotic orbits are
generated by an extremum of a map. Therefore singularities (painted in the
red) on the bifurcation diagram appear at images of the critical point
fc on(0).
Let us denote gn(c) = fcon(0), then
go(c) = 0, g1(c) = c,
g2(c) = c2 + c, ...
The curves g0,1,...,6(c) are shown in Fig.2.
Note that attractor of the map is located between g1(c)
and g2(c) curves. If a caustic crosses the vertical
line x = 0 then
gk(c) = fcok(0) = 0.
I.e. there is a superstable period-k cycle. In the neighbourhood
of this c value there is corresponding window of regular dynamics.
Contents
Previous: Quadratic map
Next: Windows of regular dynamics scaling
updated 12 July 2006

 Fig.1 shows that caustics in distribution of points of chaotic orbits are
generated by an extremum of a map. Therefore singularities (painted in the
red) on the bifurcation diagram appear at images of the critical point
fc on(0).
Let us denote gn(c) = fcon(0), then
Fig.1 shows that caustics in distribution of points of chaotic orbits are
generated by an extremum of a map. Therefore singularities (painted in the
red) on the bifurcation diagram appear at images of the critical point
fc on(0).
Let us denote gn(c) = fcon(0), then
