Cantor-like sets
Cantor strange repeller
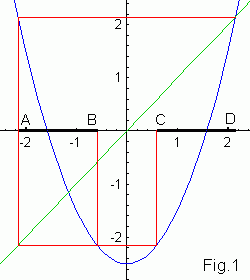
You see in Fig.1 that for c < -2 interval (BC) is mapped
outside invariant interval Ic and all points go eventually
to infinity. Two intervals [AB] and [BC] are mapped onto
Ic. So similar to the tent map
Cantor strange repeller with zero measure appears in quadratic maps.
Cantor strange repeller in regular dynamics window
We meet complicated Cantor-like structures for c = -1.7542
corresponding to period-3 window of regular dynamics. For almost all
x in interval Ic points are attracted to
period-3 orbits (these points lie in black circles). All the rest points
(after cutting these circles) make Cantor strange repeller with
zero measure. It includes unstable periodic orbits and chaotic continuum.
The basic dichotomy for real quadratic maps
For almost every c in [-2, 1/4], the quadratic map
fc : x → x2 + c is either regular
or stochastic [1]
For quadratic maps it is proven that the set of c values for which
attractor is chaotic has positive Lebesque measure and attracting periodic
orbits are dense in the set. I.e. between any two chaotic parameter values
there is always a periodic interval.
"Fat" Cantor sets
We will get a general Cantor set if in the "1/3 cutting" process we cut the
central 1/3 piece, then i.g. 1/9, then 1/27, etc.
Resulting set is topologically equivalent to the standard Cantor set, but as
since holes decrease in size very fast therefore the "fat" Cantor set has
positive Lebesque measure and fractal dimension 1 .
In the real interval -2 < c <1/4 , regions with chaotic dynamics
have nonzero Lebesgue measure and make a "fat" Cantor set. You can see below
that regular dynamics regions (black M-midgets) are dense on real axis.
[1] Mikhail Lyubich
The
Quadratic Family as a Qualitatively Solvable Model of Chaos
Notices of the AMS, 47, 1042-1052 (2000)
Contents
Previous: Transition to chaos through intermittency
Next: "Transient" chaos
updated 8 Nov 2006
|
