Period doubling bifurcations
Period doubling bifurcation for real quadratic maps
For c < 1/4, after the tangent bifurcation,
the x1 fixed point of the quadratic map (the left
intersection of fc and the green line) stays attracting
while its multiplier
|λ1 | < 1 .
For c < -3/4 it is λ1 =
1 - (1 - 4c)½ < -1 so the fixed point becomes repelling
and an attracting period-2 orbit appears.
This phenomenon is called the period doubling bifurcation.
To watch the birth of the period-2 orbit consider the two-fold iterate
f o2(x) = f(f(x)) of the quadratic map.
It is evident that two fixed points of fc are the fixed
points of fco2. Moreover as since for
these points (fco2)' =
(fc')2, therefore for -3/4 < c < 1/2
the left fixed point of fco2 is attracting
(to the left below). At c = -3/4 it loses stability
and two new intersections of fco2 with
the green line simultaneously appear (see to the right). These
x3 , x4 points make a period-2 orbit.
When this cycle appears f o2(x3 )' =
f o2(x4 )' = 1 and the slope decrease as c
is decreased.
A period doubling bifurcation is also known as a flip bifurcation,
as since the period two orbit flips from side to side about its period
one parent orbit. This is because f ' = -1 .
At c =-5/4 the cycle becomes unstable and a stable period-4 orbit
appears. Period doubling bifurcation is called also the pitchfork
bifurcation (see below).
Period doubling bifurcation on complex plane
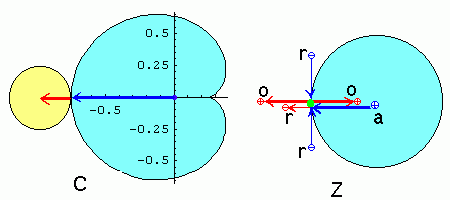
These pictures illustrate this process on complex plane.
While c is changed from c = 0 to c = -3/4
(inside the main cardioid) attractor z1
moves from 0 to the parabolic point p = -1/2 (with
multiplier λ = -1 ). Two points of
an unstable period 2 orbit are
z3,4 = -1/2 ± i t,
t = (3/4 + c)½ > 0.
Therefore they move towards the point p too from above and below.
At c = -3/4 attractor meets
the repelling orbit and they merge into one parabolic point.
For c < -3/4, since c leaves the main cardioid
and gets into the biggest (1/2) bulb, attractor turns into repeller
and the unstable period-2 orbit becomes attracting with two points
z3,4 = -1/2 ± t,
t = (-3/4 - c)½.
The right picture above is disconnected Cantor dust. We get it if we
will go up after crossing the p point.
Contents
Previous: Tangent bifurcations
Next: Period trippling bifurcations
updated 12 Sep 2013


