 We consider two-dimensional (2D) electron gas, e.g. in MOSFET on silicon or
GaAs/AlGaAs HEMT. Electron motion perpendicular to the layer (z axis) is
quantized, therefore electron energy is
We consider two-dimensional (2D) electron gas, e.g. in MOSFET on silicon or
GaAs/AlGaAs HEMT. Electron motion perpendicular to the layer (z axis) is
quantized, therefore electron energy is
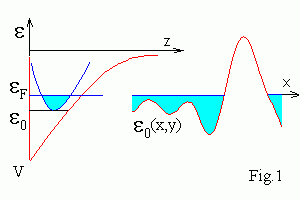
ε = εk + (Px2 + Py2)/2m*
where εk is the energy of the k-th quantum state, Px,y are components of momentum along the layer, m* is the effective mass of electron. In degenerate n-type semiconductors at low temperature T << (εF -εo ) , electron states under Fermi energy εF are filled and states with energy ε > εF are empty (see Fig.1).
Potential V(x,y) fluctuates due to presence of disorder. If de Broglie wave length of electron λ is much less, then typical scale of fluctuations, then electron motion can be treated semi-classically. These fluctuations lead to fluctuations of εo(x,y). Therefore the whole plane (x,y) is divided into filled by electrons conducting regions with εF > εo and isolated regions with εF < εo . For small εF values only the most deep valleys are filled. They are isolated and current is absent. The structure is conducting only when there is infinite extending cluster. From symmetry it follows, that percolation threshold is equal to <V> for infinite systems.
Contents
updated 21 Nov 2015