Nonlinear resonance
Here universality of the standard map dynamics is motivated. At first
we remind nonlinear pendulum dynamics. Then appearance of resonances
in nonlinear systems and single resonance approximation are explained
briefly. You can read this in any textbook and go directly to the
Standard map.
Nonlinear pendulum
Hamiltonian and equations of motion for nonlinear pendulum are
H(p,x) = p2/2 + V(x)
= p2/2 + Vo cos x = E = const
dx/dt = ∂H/∂p = p ,
dp/dt = -∂H/∂x = Vo sin x .
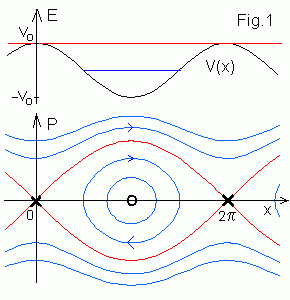 When -Vo < E < Vo particle oscillates
between two turning points. On the phase plane (x, p) its orbit rotates
periodically (blue oval curves to the left) around elliptic
fixed point O (equilibrium position at x = π ).
For E > Vo orbits pass
over maxima of V(x) and go to infinity.
The motion is unbounded. As since V(x) is periodic,
therefore we can consider motion on a cylinder and join the
0 and 2π points.
The red separatrix (or homoclinic orbit) at E =
Vo separates these two regions. It goes out and come to
hyperbolic points X (unstable equilibrium positions at x =
2pn ). Dynamics near homoclinic orbits
is very sensitive to perturbations because a small force can throw orbit
over (or under) maximum of V(x) and change qualitatively its motion.
The "width" of the homoclinic orbit is
When -Vo < E < Vo particle oscillates
between two turning points. On the phase plane (x, p) its orbit rotates
periodically (blue oval curves to the left) around elliptic
fixed point O (equilibrium position at x = π ).
For E > Vo orbits pass
over maxima of V(x) and go to infinity.
The motion is unbounded. As since V(x) is periodic,
therefore we can consider motion on a cylinder and join the
0 and 2π points.
The red separatrix (or homoclinic orbit) at E =
Vo separates these two regions. It goes out and come to
hyperbolic points X (unstable equilibrium positions at x =
2pn ). Dynamics near homoclinic orbits
is very sensitive to perturbations because a small force can throw orbit
over (or under) maximum of V(x) and change qualitatively its motion.
The "width" of the homoclinic orbit is
max Δp = 4 V o½.
Resonances
For canonical action-angle variables (I, θ)
Hamiltonian H(I) depends on I only and equations of motion are
dI/dt =
-∂H(I)/∂θ = 0 , I = const ,
dθ/dt = ∂H(I)/∂I = ω(I) =
const .
Under a periodic perturbation V(I, θ, t) = V(I, θ, t + T)
H(I, θ, t) =
Ho(I) + εV(I, θ, t) = Ho(I) +
ε∑ n,m Vnm(I) einθ -
imΩt ,
dI/dt = -∂ H/∂ θ =
-iε∑ n,m nVnm(I) einθ -
imΩt , (*)
dθ/dt = ∂ H/∂ I .
where Ω = 2π /T.
For small ε we will search solution as a series
I = I o + εI 1 + ... ,
θ = θ o + εθ 1 + ... ,
I o = const,
θ o = ω(I o)t .
After substitution I o, θ o
into (*) we get
dI 1/dt =
-i∑ n,m nVnm(I o)
exp[i(nω(I o) - mΩ)t] ,
I 1 =
-∑ n,m nVnm(I o)
/[nω(I o) - mΩ]
ei[nω(I o) - mΩ]t + const .
At a resonance nω(I) - mΩ = δnm ~ 0 ,
I 1 and θ 1
contain divergent terms with small denominators
Vnm /δnm.
In nonlinear systems frequency ω(I) depends on I,
therefore we can get resonanses at any external frequency Ω
for some I, n, m.
Single resonance approximation. Universal Hamiltonian
To avoid this divergence for a single resonance we can solve (*) taking
into account only secular terms with nω - mΩ ~ 0
dI/dt = εnVnm
sin(nθ - mΩt + φ) ,
dθ/dt = ω(I) + ε dVnm/dI
cos(nθ - mΩt + φ) .
Corresponding Hamiltonian is
H = Ho(I) + εVnm(I)
cos(ψ), ψ = nθ - mΩt + φ.
For small ΔI = I - Io
it turns into the nonlinear pendulum Hamiltonian
H(ΔI, ψ) = nω' ΔI 2/2 +
nεV cos( ψ ) ,
ω' = dω/dI .
Thus independently on ω(I), V(I)
dynamics near resonance is described approximately by this universal
Hamiltonian. Resonant terms lead to appearence of homoclinic orbits
on the (ψ, ΔI) phase plane (similar to Fig.1) with the width
max ΔI = 4 (εV/|ω'|)1/2 .
Nonresonant terms lead to chaotic dynamics near homoclinic orbits.
To see this we can plot Poincare sections of the flow at the moments
t = n T . One model example is the standard map below.
You see resonances, invariant circles and chaos near homoclinic orbits.
Contents
Previous: Strange attractors
Next: The Standard map
updated 26 August 2003
 When -Vo < E < Vo particle oscillates
between two turning points. On the phase plane (x, p) its orbit rotates
periodically (blue oval curves to the left) around elliptic
fixed point O (equilibrium position at x = π ).
For E > Vo orbits pass
over maxima of V(x) and go to infinity.
The motion is unbounded. As since V(x) is periodic,
therefore we can consider motion on a cylinder and join the
0 and 2π points.
The red separatrix (or homoclinic orbit) at E =
Vo separates these two regions. It goes out and come to
hyperbolic points X (unstable equilibrium positions at x =
2pn ). Dynamics near homoclinic orbits
is very sensitive to perturbations because a small force can throw orbit
over (or under) maximum of V(x) and change qualitatively its motion.
The "width" of the homoclinic orbit is
When -Vo < E < Vo particle oscillates
between two turning points. On the phase plane (x, p) its orbit rotates
periodically (blue oval curves to the left) around elliptic
fixed point O (equilibrium position at x = π ).
For E > Vo orbits pass
over maxima of V(x) and go to infinity.
The motion is unbounded. As since V(x) is periodic,
therefore we can consider motion on a cylinder and join the
0 and 2π points.
The red separatrix (or homoclinic orbit) at E =
Vo separates these two regions. It goes out and come to
hyperbolic points X (unstable equilibrium positions at x =
2pn ). Dynamics near homoclinic orbits
is very sensitive to perturbations because a small force can throw orbit
over (or under) maximum of V(x) and change qualitatively its motion.
The "width" of the homoclinic orbit is