w = u + i v = (n1 + i n2)/(1 - n3) = ctg(θ/2) eiφ.
Отметим, что все бесконечно удаленные точки плоскости отображаются в одну точку - "северный" полюс сферы. Используя соотношения


|
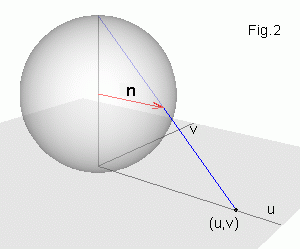
При помощи стереографической проекции каждой точке сферы
n = (sin θ cos φ, sin θ sin φ, cos θ)
можно поставить в соответствие точку на плоскости w = (u, v)
w = u + i v = (n1 + i n2)/(1 - n3) = ctg(θ/2) eiφ. Отметим, что все бесконечно удаленные точки плоскости отображаются в одну точку - "северный" полюс сферы. Используя соотношения |
3D VRML модели полей (смотри
Why VRML?):
инстантон с α=0, антиинстантоны с
α=0, α=1.5,
"чупа-чупс". 3D модели полезны для общего ознакомления,
но плоские картинки кажется мне более информативными.
Приведенный ниже Java аплет строит вид сверху на векторное поле антиинстантона
с фазой α = 0 . По краям приведен вид сбоку на сечения вдоль
горизонтальной и вертикальной серых линий. Красным цветом изображены
вектора, которые направлены на наблюдателя, синие вектора направлены от него.
w(∞) → 1 что соответствует направлению поля на бесконечности
прямо на нас. Направлению строго от нас соответствует w(zo) =
-1 . Откуда следует, что "полюс" (синяя точка на картинке) расположен
в zo = eiα/2 . Наконец для векторов
лежащих строго в плоскости рисунка Re(w) = 0 , что соответствует
окружности с радиусом 1/2 и центром в полюсе, проходящей через начало
координат. Внутри окружности стрелки (голубые) направлены он нас, а
снаружи на нас.
Управление:
Щелкните изображение мышкой с Alt (Ctrl) чтобы растянуть (сжать)
картинку в 2 раза. Чтобы сдвинуть перекрещивающиеся серые линии потяните их
мышкой. Координаты пересечения видны в строке состояния (внизу окна).
Нажмите Enter чтобы ввести новое значение фазы (поле a).
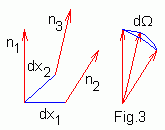
| Для трех близких векторов n(x), n(x+dx1) и n(x+dx2) площадь "занимаемая" на сфере Sn2 равна величине телесного угла dΩ образованного этими векторами. Для бесконечно малых dx1, dx2 телесный угол пропорционален объему, заключенному между этими векторами (n ·[∂1n , ∂2n]) dx1 dx2 . |
Но если (по аналогии с вихрями) область
пространства с Гейзенберговским ферромагнетиком окружить сферой и задать на
ней ненулевой топологический заряд (простейшая ситуация, когда все стрелки
торчат наружу по радиусу - т.е. "ежик"), то:
Что будет находиться внутри - монополь?
Чему они будут дуальны, если поле принимает значения на сфере, а не в U(1)?
Будут ли притягиваться Q = 1 и Q = -1 и как? :) ...
Я благодарен Д.Е.Бурланкову за полезные обсуждения.
[1] А.А.Белавин, А.М.Поляков Метастабильные состояния двумерного
изотропного ферромагнетика. Письма в ЖЭТФ, 22(10), 503 (1975).
[2] А.М.Переломов Решения типа инстантонов в киральных моделях.
УФН 134, 577, (1981)