P '(0) = 3(P1 - P0) , P '(1) = 3(P3 - P2) ,
P "(0) = 6(P0 - 2P1 + P2) , P "(1) = 6(P1 - 2P2 + P3) .
Note also, that for any two points a and b the point (2a - b) =
a + (a - b) is "mirror b with respect to a".

|
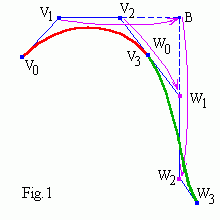
Earlier we built C1 continuous
Cardinal spline. Now we will make a piecewise
C2 continuous uniform B-spline of two cubic Bezier
segments V(t) and W(t) with the control points
(V0 , V1 , V2 ,
V3) and (W0 , W1 ,
W2 , W3) (see Fig.1).
Recall that for cubic Bezier spline
P '(0) = 3(P1 - P0) , P '(1) = 3(P3 - P2) , P "(0) = 6(P0 - 2P1 + P2) , P "(1) = 6(P1 - 2P2 + P3) . Note also, that for any two points a and b the point (2a - b) = a + (a - b) is "mirror b with respect to a". |
From Fig.2 it follows, that one can express all control points of Bezier
segments in terms of the deBoor points P0,1,...,n
(the corners) , e.g.
V1 = P1 +
(P2 - P1)/3 =
(2P1 + P2)/3 ,
V0 =
[(P0 + 2P1)/3 +
(2P1 + P2)/3]/2 =
(P0 + 4P1 + P2)/6 .

Then Bezier segments points can be computed. But one can evaluate
points of k-order B-spline directly by the Cox - beBoor
algorithm similar to deCasteljau iterations
Pir =
Pir-1 (t - ti)/(ti+k-r -
ti) +
Pi-1r-1 [1 - (t - ti)/(ti+k-r
- ti)] ,
where ti are knots, which determine the start and end of
each segment. Bezier segments have local coordinates
τi =
(t - ti)/(ti+1 - ti),
0 < τi < 1 ,
ti < t < ti+1 .
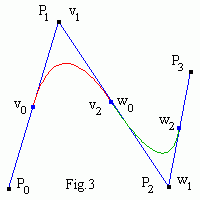
Bezier and deBoor control points of quadratic B-spline are shown in Fig.3.
Note that I've found the Cox - beBoor formula in the Net and didn't check
it (see Spline formulae standartization). I used basis
function calculation instead.