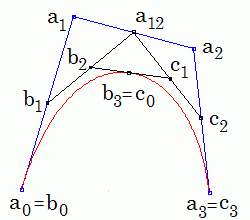
|
As we known that a cubic spline curve
with control points a0 , a1 , a2 ,
a3 can be subdivided in two sub curves with control points
b0 , b1 , b2 , b3 and
c0 , c1 , c2 , c3
as shown to the left
function subdiv(a0,a1,a2,a3){
var b1 = av(a0,a1), a12 = av(a1,a2), b2 = av(b1, a12),
c2 = av(a2,a3), c1 = av(a12,c2), b3 = av(b2,c1);
return [[a0,b1,b2,b3],[b3,c1,c2,a3]];
}
function av(v1, v2){
return [.5*(v1[0]+v2[0]), .5*(v1[1]+v2[1]), .5*(v1[2]+v2[2])];
}
where av(v1, v2) is the midpoint between v1 and v2.
|
