
Solution: The top three are the same, up to isomorphism; and the bottom three are the same up to isomorphism. The bottom three are not isomorphic to the top three.
Definition 1: Two graphs: G = (V, E) and G' = (V', E') are called isomorphic if there is a one-to-one mapping f from V onto V' such that any two vertices v1, v2 V are adjacent iff f(v1) and f(v2) are adjacent.
Definition 2: The complement of a graph G has V(G) as its vertex set; two vertices are adjacent iff they are not adjacent in G. A graph G is called self-complimentary if G is isomorphic to .
Definition 3: The edge graph, or the line graph L(G) of a G is the graph with vertex set E(G) in which two vertices are adjacent iff they are adjacent as edges in G.
Problem 4: How different are these graphs?

Solution: The top three are the same, up to isomorphism;
and the bottom three are the same up to isomorphism. The bottom three are not
isomorphic to the top three.
Problem 5: Are the graphs below isomorphic? Explain.
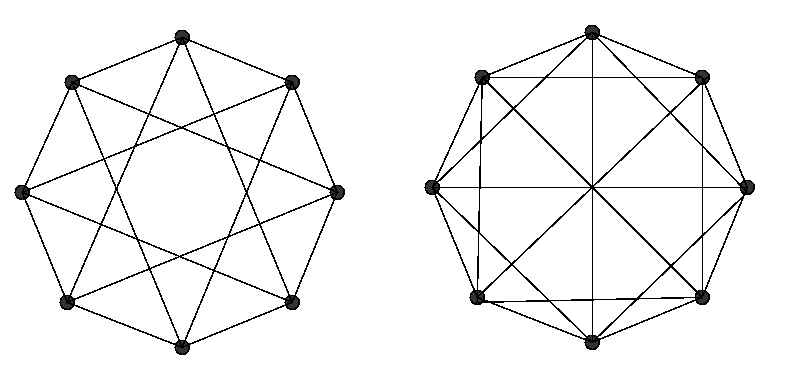
Solution: The two graphs are not isomorphic, since the
degrees of vertices in the left one are 4, while the degrees of the right one
are 5.
Problem 6: Construct all non-isomorphic graphs with
4 vertices. Construct all non-isomorphic regular graphs with 4 and 5 vertices.
Construct a 3-regular graph with 11 vertices.
Solution: The list of all non-isomorphic graphs with
4 vertices:
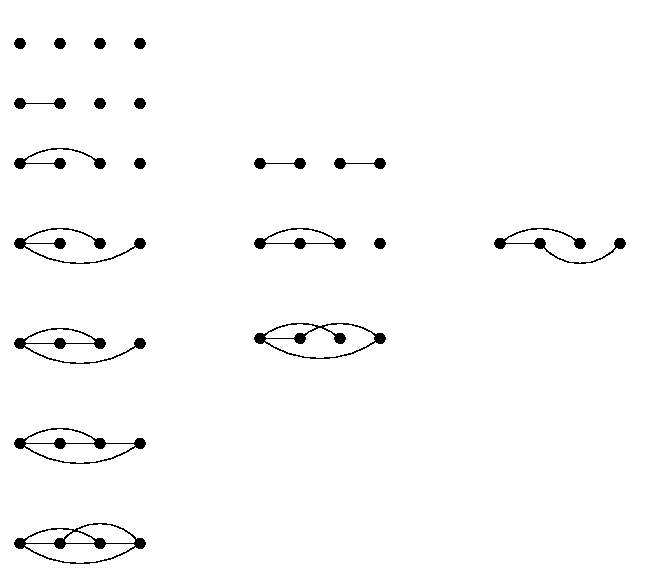
There are three regular graphs with four vertices.
There are exactly four regular graphs with five vertices. One such graph is
of degree zero, the empty graph; the other one is the complete graph, whose
degree is four; it is the complement of the empty graph. No 5-vertex graph of
degree two is a 5-cycle; it is a self-complementary graph.
Problem 7: Determine wich pairs of the graphs below
are isomorphic. Are any of these graphs isomorphic to
?
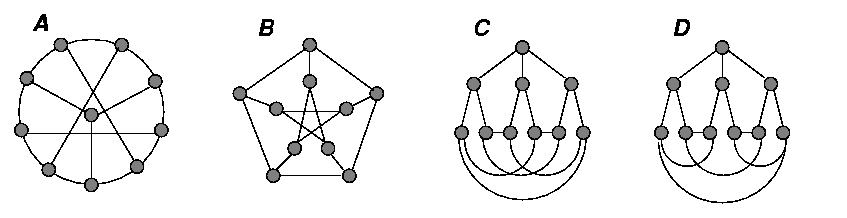
Solution: Graphs A, B, and C, but not
D are isomorphic to
.
Problem 8: Determine which pairs of the graphs below
are isomorphic.
Solution: Graphs B and C are isomorphic
and neither are isomorphic to A.
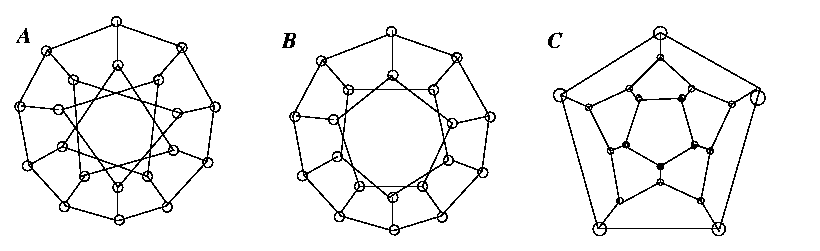
Problem 9: Determine which pairs of the graphs below
are isomorphic.
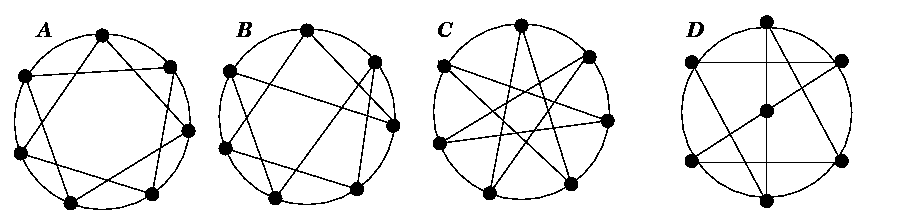
Solution: Every vertex of A belongs to three triangles;
some but not all vertices in B belong to three triangles; none of the
vertex in C belongs to three triangles. Thus, A, B, and C
are not isomorphic to each other. A is isomorphic to D.
Problem 10: The vertices of graph Ok are thek-element subsets of {1,2,...,2k + 1}. Two vertices are adjacent iff the are disjoint sets. Prove that
Problem 11: If G is self-complimentary, then |V(G)| is either 4k or 4k + 1 for some k 0.
| Solution: If e and v are, respectively, the number of edges and the number of vertices of G, then for a self-complimentary G, |
|
|
| Therefore, 4e = v(v-1), which implies the result. |
Problem 12: Construct all non-isomorphic graphs with five vertices. There are exactly 34.
Solution: This problem should be solved by writing a computer program. Such a solution is acceptable if the corectness of the program is checked.
Definition 13: A one-to-one mapping f : V(G) V(G) is called automorphism, if any two vertices x, y V(G) are adjacent iff f(x), f(y) are adjacent.
Problem 14: Construct a 3-regular graph with 12 vertices in which the identity is the only automorphism.
|
|
| The reverse is also true. |
Theorem 16: (Havel and Hakimi, 1963) Let d = {d1, d2,...,dn) be a non-increasing sequence of non-negative integers. Denote d' the sequence {d2 - 1, . . . ,dd + 1 - 1, dd1 + 2, . . . , dn}. Then d is a degree sequence of a graph iff d' is.
Problem 17: Construct a graph with degree sequence {5, 3, 2, 2, 2, 1, 1}. There are four.
Solution:

Problem 18: How many are graphs with degree sequences {6, 6, 5, 4, 3, 3, 1}?
Solution: None.
Problem 19: How many are graphs with the degree sequences {7, 6, 5, 4, 3, 2}?
Solution: None.
| Problem 20: Show that the edge graph L(G) has |E(G| vertices and |
|
|
| edges. |
Definition 21: If G and H are vertex-disjoint
graphs then
- the union G H is the graph V(G) v(H), E(G) E(H));
- the join G + H is the graph obtained from G H by adding all edges (v, u) where v V (G) and u V(H).
- the product G x H is the graph F with V(F) = V(G) x V(H) and E(F) = {((v, u1), (v, u2))} {((x1, y), (x2, y))}, where (u1, u2) E(H), v V(G) and y V(H), (x1, x2) E(G)).
- the Cartesian product G H is the graph F with V(F) = V(G) x V(H) and E(F) = {v1, u1), (v2, u2))} where ((v1, v2) E(G) and (u1, u2) E(H).
Definition 22: A decomposition of a graph is a list of subgraphs such that each edge appears in exactly one subgraph in the list.
|
Problem 23: Prove or disprove:
|
Problem 24: How to represent a hypercube (or an n-cube) Qn using the product operation?
Problem 25: Decompose K5 into two 5-cycles.
Problem 26: Decompose K7 into seven K3.
Problem 27: Decompose P (Petersen graph) into three connected subgraphs that are pairwise isomorphic.
Problem 28: Prove that if Kn decomposes into triangles, then either n - 1 or n - 3 is divisible by 6.