Dijkstra's Algorithm
Dijkstra's algorithm solves the single-source
shortest-path problem on a weighted graph (directed or undirected),
provided all edge-weights are nonnegative.
Dijkstra's algorithm maintains a set of vertices whose final
shortest-path weights from the source have already been calculated,
along with a complementary set of vertices whose shortest-path weights
have not yet been determined. The algorithm
repeatedly selects the vertex with the minimum current shortest-path
estimate among those whose shortest-path weights have not yet been
determined. It updates the weight estimates to all vertices adjacent
to the currently selected vertex (this updating is commonly referred
to as "relaxation" of the edges between these vertices). The vertex
is then added to the set of vertices whose final shortest-path weights
have been calculated.
It continues to do this until all vertices' final shortest-path
weights have been calculated (until the set of vertices whose
shortest-path weights have not been determined is empty).
The Algorithm
-
 is the set of vertices
is the set of vertices
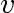 for which the distance from
for which the distance from
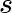 to
to
 has been computed.
has been computed.
-
 is the set of vertices
is the set of vertices
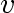 for which the distance from
for which the distance from
 to
to
 has not yet been computed.
has not yet been computed.
-
 is the current estimate of the weight from vertex
is the current estimate of the weight from vertex
 to vertex
to vertex
 . .
-
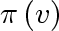 is a predecessor of
is a predecessor of
 .
In other words, the vertex through which the shortest distance from .
In other words, the vertex through which the shortest distance from
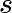 to to  was established. was established.
 while
while
 {
Find {
Find
 with the smallest
with the smallest
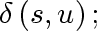
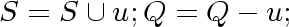 for every
for every
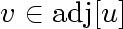 if
if
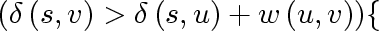

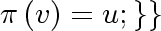
| 


