EX2: Cylindrical Shell
4: Cylindrical Geometry (Example 2)
A hollow cylinder has circular inner and outer surfaces. The cross-section, shown
in Figure 3, is a ring of inner radius
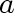 and outer radius and outer radius
 . We
consider two cases of symmetric, steady state boundary conditions in which the
temperature distribution depends on one space variable. As in , the conductivity . We
consider two cases of symmetric, steady state boundary conditions in which the
temperature distribution depends on one space variable. As in , the conductivity
 is assumed to be constant. is assumed to be constant.
 Figure 2: Figure 2: 2a. FLOW ALONG THE CYLINDER
Suppose that the cylindrical tube has finite length
 , with plane end
faces perpendicular to the axis of the tube, and that the lateral (curved)
surfaces are insulated. Let each face be maintained at a constant temperature,
one at , with plane end
faces perpendicular to the axis of the tube, and that the lateral (curved)
surfaces are insulated. Let each face be maintained at a constant temperature,
one at
 and the other at and the other at 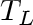 . We define
the x-axis to coincide with the tube's axis, with the ends of the tube lying
in the planes . We define
the x-axis to coincide with the tube's axis, with the ends of the tube lying
in the planes
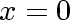 and and
 , such that , such that
 at at
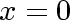 and and
 at at
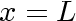 . (See Figure 4.) . (See Figure 4.)
Since the lateral surfaces are insulated there is no heat flow through these
curved walls; in other words, the heat flux vector
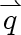 has a zero component normal to the walls. In fact, it can be shown, as
in Example 1, that
has a zero component normal to the walls. In fact, it can be shown, as
in Example 1, that
 is always in the x-direction. Then an argument similar to that in Example
1 yields in this case the same expressions for the rate of heat flow and temperature
distribution, given by equations (3.4) and (3.5).
is always in the x-direction. Then an argument similar to that in Example
1 yields in this case the same expressions for the rate of heat flow and temperature
distribution, given by equations (3.4) and (3.5).
 Figure 3: Figure 3: 2b. RADIAL FLOW
Now suppose that the cylindrical tube, of inner radius
 and outer radius and outer radius
 , has infinite length, and that the inner cylindrical surface is maintained at constant temperature , has infinite length, and that the inner cylindrical surface is maintained at constant temperature
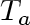 , the outer at constant temperature , the outer at constant temperature  . We wish to determine
the temperature distribution and the direction and magnitude of the heat flow within the material. . We wish to determine
the temperature distribution and the direction and magnitude of the heat flow within the material.
Since
 has constant values on each of the cylindrical surfaces has constant values on each of the cylindrical surfaces
 and and
 , the temperature varies in the radial direction,
depending only on , the temperature varies in the radial direction,
depending only on
 , and heat flows in the radial direction. , and heat flows in the radial direction.
The most convenient coordinates for this geometry are cylindrical
coordinates, consisting of polar coordinates
 in a cross-sectional plane and a third (Cartesian) coordinate along the axis
of the cylinder. In this problem we do not need the complete form of the
gradient in cylindrical coordinates. Here the temperature and heat flow
depend only on
in a cross-sectional plane and a third (Cartesian) coordinate along the axis
of the cylinder. In this problem we do not need the complete form of the
gradient in cylindrical coordinates. Here the temperature and heat flow
depend only on
 , in which case , in which case
 reduces to a single term: reduces to a single term:
 Equation
17
Equation
17
The vector
 denotes a unit vector in the r (radial) direction.
denotes a unit vector in the r (radial) direction.
Let us restrict our attention to a tube of finite (unit) length. In
this tube consider a cylindrical surface of radius
 , which we call , which we call
 . On . On
 (that is, for fixed (that is, for fixed
 ) )
 is constant and the heat flux vector is constant and the heat flux vector
 (normal to the cylinder) has a constant magnitude (normal to the cylinder) has a constant magnitude
 . Since the area of . Since the area of
 is is
 (the tube is of unit length), the rate of heat flow through
(the tube is of unit length), the rate of heat flow through
 (in watts) is (in watts) is
 . Heat flows outward if . Heat flows outward if
 has positive sign. has positive sign.
Because this is a steady state process, the rate of heat flow through
 is the same for all is the same for all
 , ,
 . In other words, . In other words,
 (a constant which we determine below), or
(a constant which we determine below), or
 Equation
18
Equation
18
Note that the heat flux varies inversely with
 ; in other words, ; in other words,
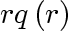 is constant.
is constant.
Using equations (4.1) and (4.2) to substitute for
 and and
 in the heat conduction law, in the heat conduction law,
 , we obtain the simple differential equation , we obtain the simple differential equation
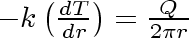 Equation
19
Equation
19
A differential equation is an equation
containing a derivative of an unknown function with respect to an
independent variable. Equation (3.3),
 , is also a
differential equation, even simpler than (4.3), for the right hand
side of (3.3) is a
constant. , is also a
differential equation, even simpler than (4.3), for the right hand
side of (3.3) is a
constant.
| 


