Vi = ∑j= -Rc,Rc fi+j

|
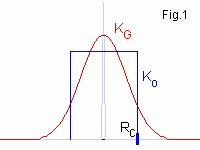
Независимые случайные точки fi с
равномерным распределением на интервале (-1, 1) образуют белый шум
(голубая кривая). Коррелированные случайные точки Vi
(красная кривая) получены усреднением белого шума в сфере с радиусом
Rc , т.е. используется интегральное ядро
Ko
Vi = ∑j= -Rc,Rc fi+j |

Фрактальный шум. Нажмите Enter чтобы ввести новое значение
m.
Чтобы получить 2D фрактальный шум (или "горный ландшафт"), возьмите резиновую нить (см. Fig.1) и сместите случайным образом ее центральную точку. Далее повторите этот процесс рекурсивно к каждому из двух новых сегментов. Случайное смещение уменьшается на величину m при каждой новой итерации (обычно используется m = 2).
|
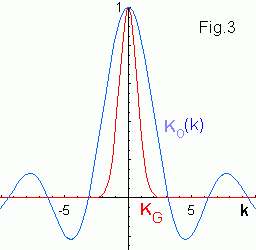
Разлагая V(r), K(r), f(r) в ряд Фурье
g(k) = ∫ g(r) eikr dr , получим для V(k) V(k) = K(k) f(k) . Т.о. усреднение в (*) означает пропускание белого шума через фильтр с полосой пропускания K(k). Полосы пропускания для двух использованных фильтров (для Rc = 1) приведены на Fig.3 KG(k) ~ exp[-(Rck)2], Ko ~ sin(Rck)/k. |
И, наконец, двумерный коррелированный случайный потенциал. Чтобы получить
гладкий потенциал использовано двумерное гауссово ядро.
Протекание в случайном потенциальном рельефе
Вы можете повернуть 3D картинку с помощью мыши ("потащите" мышку с "shift",
чтобы увеличить/уменьшить масштаб). Белая линяя в голубой полосе справа
показывает положение среднего потенциала <V>. Желтая линяя
соответствует энергии Ферми εF .
Потащите эту линию мышкой, чтобы изменить значение
εF . См. также
3D Mountains и
Hidden Surface Removal Algorithms