Метод ренорм-группы
Универсальность протекающего кластера
Слева внизу вы видите протекание по узлам, а справа
континнуальное протекание в случайном потенциале
при p = pc .
Перебрав несколько случайных реализаций вы можете убедиться, что протекающие
(бесконечные!) кластеры слева и справа очень похожи и действительно не зависят
от структуры решетки на малых масштабах. Это приводит к универсальности
поведения различных систем (и критических индексов) на плоскости вблизи точки
фазового перехода.
Перенормировка
Идею изучения некоторых физических в окрестности критических точек на
различных масштабах длины (метод ренорм-группы) предложил в
1971 г. К.Ж.Вильсон. Проще всего познакомиться с этим методом на примере
задач перколяции. Для этого сожмем "бесконечную" решетку (например квадратную
решетку налево вверху) в b раз. Чтобы можно было
сравнивать изображения на старой и новой решетках, размер ячеек сжатой решетки
нужно увеличить в b раз, т.е. нужно провести "огрубление" кластеров
новой решетки.
|
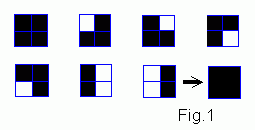
На рисунке слева показана процедура "огрубления" протекания при b = 2 ,
т.е. группировки ячеек в блоке 2х2 и замене их единственной ячейкой. Каждая
из 7 протекательных конфигураций заменяется на большой черный квадрат,
остальные конфигурации - на белый.
|
.gif)
|
Если исходные ячейки были заняты с вероятностью p, то вероятность
протекания блока в данном случае [1]
p' = R(p) = p4 +4p3(1-p) +
2p2(1-p)2 .
При p < pc p' < p поэтому
ниже вы видите, что последовательное применение преобразования перенормировки
при p = 0.5 < pc приводит к исчезновению черных квадратов
после 3 итераций (т.е. p' -> 0 ). Отметим, что перенормированные
решетки внизу не сжимаются, чтобы было удобнее следить за огрублением.
Наоборот при p > pc
останутся только черные квадраты (p' -> 1 ).
|
Наконец при p = pc предполагается, что в системе существуют
все масштабы длины и изменение масштаба не играет роли (т.е. картинка будет
выглядеть одинаково независимо от масштабного преобразования). Это соответствует
неподвижной точке уравнения p* = R(p* ) при
p* = 0.61803 , что действительно очень близко к критическому
значению pc = 0.5927 .
Точность полученных результатов увеличивается с ростом b. Однако,
поскольку имеется 2b2 возможных конфигураций
для клетки размером bxb , число которых быстро растет с ростом
b, для b > 5 используется метод Монте-Карло.
Критический показатель
ν
Разлагая R(p) в ряд Тейлора получим связь между p и p'
вблизи от неподвижной точки p*
p' - p* = R(p) - R(p*) =
dR/dp|p = p* (p - p*) =
λ(p - p*) (*)
где λ =
dR/dp|p = p* .
Для вычисления критического показателя ν
вспомним, что на ренормированной решетке все длины уменьшаются в b
раз. Следовательно длина связности l' = l/b . Поскольку
l(p) ~ |p -
pc|-ν
и pc соответствует p* , то
из соотношения для длин следует
|p' - p*|-ν
=|p - pc|-nu; /b .
Подставляя (*), после несложных вычислений получим
ν = log(b) /
log(λ) .
В рассмотренном выше случае для протекания по узлам квадратной решетки
b = 2 , λ = 1.5279 и
ν = log(2) / log(1.5279)
= 1.635...
что достаточно близко к точному значению ν =
4/3 для двумерного случая.
[1] Х.Гулд, Я.Тобочник "Компьютерное моделирование в физике" Мир,
1990 (т.2, главы 12,16)
Содержание
«Белый, коррелированный и фрактальный шум
обновлено 16 янв 2004


.gif)


