Definitions
Definitions Associated With Directed Graphs
Theorem
Let  be a labeled digraph with adjacency
matrix be a labeled digraph with adjacency
matrix 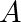 and and
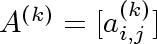 be the k-power of
be the k-power of 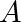 . .
Then the
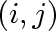 -th
entry of -th
entry of
 is the number of directed walks of length
is the number of directed walks of length  from from
 to
to
 . .
Proof
Let us prove it by induction on 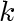 . .
Base Case: The number of directed walks of length
 is equal to
is equal to
 iff iff
 ;
since ;
since
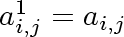 ,
the base of the induction ,
the base of the induction
 holds true.
holds true.
Inductive Step: Let the theorem be true for some
 and let us present the entries of
and let us present the entries of
 through those of
through those of
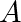 and
and
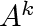 . .
Since
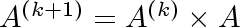 ,
we write ,
we write
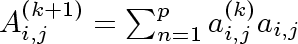 . .
Since every directed walk of length
 consists of a directed walk of length
consists of a directed walk of length
 from
from
 to
to
 for some
for some
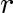 ,
followed by an edge ,
followed by an edge
 ,
we see that the equality above counts all paths of length ,
we see that the equality above counts all paths of length
 . .
| 


